Bradley-Terry Model: paired comparison models
동기
세상에는 비교할 것이 많습니다.여러분에게 3가지 옵션이 주어져 있다면 전부 세 번 비교를 할 수 있습니다.
예를 들어, 사과, 바나나, 파인애플 중에서 무엇을 더 좋아하는지 물어볼 수 있습니다.
사과를 A, 바나나를 B, 파인애플을 C라고 하면
A 와 B
B 와 C
A 와 C
이렇게 비교할 수 있습니다.
비교는 어렵지 않지만, 만약 여러분이 채식을 좋아하는지 육식을 좋아하는지에 따라 비교의 결과가 다른지 알아보려면 어떠한 방법을 써야 할까요?
Bradley-Terry의 로그선형모델(Log-Linear Bradley-Terry model, LLBT Model)을 사용하면 답을 얻을 수 있습니다.
Paired-comparison 분석 방법은 Categorical data analysis의 일종으로 연구에 응용할 수 있는 여지가 많은 분석 방법입니다.
Worth Parameter
우선 worth parameter에 대해 설명을 해야겠습니다.
위의 식은 객체 j를 객체 k보다 좋아할 확률을 계산하는 함수를 보여줍니다. 이때 계산에 사용되는 파이를 worth parameter라고 합니다. worth parameter가 주어져 있다면 선호하는 확률을 계산할 수 있다는 의미입니다. 예를 들어 j의 worth parameter가 7이고, k의 worth parameter가 3이리면 j를 k보다 좋아하는 확률은 0.7(=7/(7+3))입니다.
Design Structure
LLBT에 관련된 자세한 연구는 Fienberg & Larntz (1976)이나 Dittrich et al. (1998)을 참조하시고... 여기서는 간단히 데이터를 정리해서 {prefmod} 패키지로 LLBT를 사용하는 방법에 초점을 맞추겠습니다.
우선 Response는 결과값을 기록하는 방법입니다.
비교의 앞쪽을 선호하면 1, 뒤쪽을 선호하면 -1이라고 기록했습니다. 미리 설명하지만 {prefmod}에서는 앞쪽을 선호하면 1, 뒤쪽을 선호하면 2라고 합니다만, 설명의 편의를 위해서 1과 -1로 표기합시다.
응답자(response)는 y를 사용해서 구분하고, 각각의 의사결정에 대해 첨자로 구분했습니다. 3를 paired하면 (12, 13, 23)이 되니 각각 y_12, y_23, y_13이 됩니다.
다음으로 Counts는 선호의 개수입니다. n_(1>>2)는 1보다 2를 선호한다는 뜻이고, n_(2>>1)은 2를 1보다 선호한다는 뜻입니다.
mu_(12)나 mu_(13)은 위치를 나타내는 dummy에 불과하고, lambda_1이나 lambda_2는 선호 게임에서의 득점입니다(zero-sum이 됨을 보세요).
LLBT에서 기대치는 response의 개수와 response의 확률의 곱입니다. 그냥 평균을 구할 때와 마찬가지입니다.
이제 linear prediction을 정의합시다.
간단한 예: Factor Model
우선은 간단한 예만 소개하고 복잡한 것들은 나중에 다시 살펴봅시다.우선 R에서 {prefmod} 패키지를 설치합시다.
R> install.packages("prefmod")
R> library(prefmod)
이 패키지에 내장된 데이터 중 trdel을 사용합니다.
R> data("tradel")
데이터를 열어보면 다음과 같습니다.
변수가 V1부터 V10까지 있습니다. 이것들은 5개의 오브젝트를 비교한 결과입니다. 5개의 object를 2개씩 combination하면 5_C_2=(5*4)/(2*1)=10입니다.
각각의 비교대상(object)는
- CO: Computer-based training
- TV: TV-based training
- PA: Paper-based training
- AU: Audio-based training
- CL: Classroom-based training
이렇습니다.
Factor별로 이들 비교가 어떻게 다른가 알아보려니 Factor도 정의해야 합니다. 데이터에서 ltype이 이 factor라고 합시다.
- 1: Accomodator
- 2: Diverger
- 3: Converger
- 4: Assimilator
학습자의 성격을 분류해서 4종류로 봅니다.
오브젝트 이름을 정의하고
R> objnames <- c("CO","TV","PA","AU","CL")
LLBT paired-comparison Fitness를 계산합니다.
R> mod.tr.ltype <- llbtPC.fit(trdel, nitems=5, obj.names=objnames, formel=~ltype,elim=~ltype)
포뮬러(formel)에 predictor를 ltype으로 본다고 기록했습니다.
분석테이블을은 elim으로 설정합니다. ltype별로 분석해야 하니 elim에 포뮬러를 넣습니다.
R> summary(mod.tr.ltype)
GLM, Poisson의 결과를 보여줍니다. 전체적으로 CO가 가장 선호되는 것을 볼 수 있습니다. 이제 worth parameter를 구해서 원래 우리가 해보고 싶은 결과를 얻어 봅시다.
R> w <- llbt.worth(mod.tr.ltype)
R> colnames(w) <- c("Accomodator","Diverger","Converger","Assimilator")
R> plot(w, log='y')
독립변수가 factor라면 위와 같이 간단히 worth parameters를 구할 수 있습니다.
하지만, 독립변수가 "나이"와 같은 연속변수라면 사정이 좀 복잡합니다.
Design space를 구성해야 합니다.
미리 보여드렸다시피 쌍대비교를 일일이 다 설계해야 하기 때문에 번거롭고 복잡합니다. {prefmod}는 이것을 자동으로 처리합니다.
R> dsg <- llbt.design(trdel, 5, objnames=objnames, num.scovs="age")
문자 scovs는 subject covariates의 약자입니다. num은 numerical, 즉 수치자료라는 뜻입니다. 나머지는 간단히 아시겠지요?
이제 볼까요?
R> Views(dsg)
Responses가 y이고, mu는 더미입니다. 람다에 해당되는 것들이 CO, TV, PA, AU, 그리고 CL입니다. 이것들은 zero-sum입니다. 위상을 표시하는 뮤가 g0, g1로 표기되었습니다.
원래 trdel의 자료 크기는 198개에 불과하지만, 쌍대비교의 design 행렬의 크기는 무려 3,960개나 됩니다. 198개 비교값이 10회이고 쌍대이니, 전체 크기는 198*10*2=3960개로 늘어났습니다.
이제 비선형모형을 작성해서 worth parameters를 계산합시다.
R> mod.tr.age <- gnm(y ~ (CO+TV+PA+AU+CL)*age, family=poisson, eliminate=mu:CASE, data=dsg)
R> mod.tr.age
비선형모형의 구조를 eliminate에 넣습니다. 수치형공분산을 반영했기에 mu:CASE를 넣었습니다.
Worth parameter를 그냥 구할 수는 없고....
R> est <- parameters(mod.tr.age)
R> estmat <-do.call("cbind", lapply(15:55,function(x) est[1:5]+est[7:11]*x))
R> wmat <- apply(estmat, 2, function(obj) exp(2*obj)/sum(exp(2*obj)))
객체 wmat이 worth parameter입니다.
그래프를 그려보겠습니다.
R> col <- rainbow_hcl(5)
R> plot(c(10,60),range(wmat),type='n')
R> for (i in 1:5) lines(15:55, wmat[i, ], col=col[i])
R> text(rep(10,5), wmat[,1], objnames)
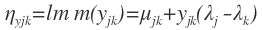
댓글
댓글 쓰기