Variance가 높을 경우? 디리슈레-다항분포 회귀식 사용

(본 내용은 Erik Thorsen의 "Multinomial and Dirichlet-multinomial modeling for categorical time series"를 바탕으로 작성했음을 밝힙니다.)

Multinomial distribution을 사용하여 다음과 같은 경우의 회귀분석을 하려고 합니다.

"연령별 로타바이러스(RotaVirus)에 취약한 정도를 알고 싶다!"

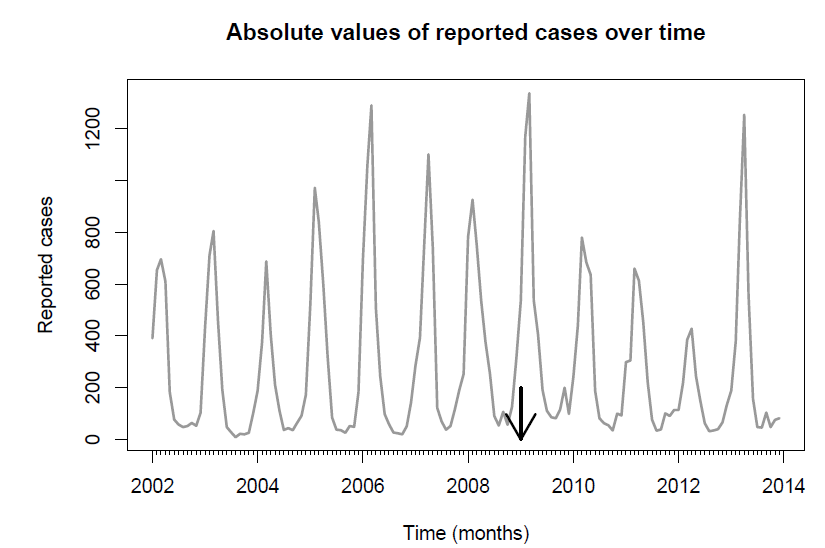
로타바이러스는 구토 설사 발열을 유발하는 고약한 놈으로 알려져 있고 주로 영유아에서 많이 발생한다고 합니다. 2000년부터 2014년에 이르는 기간 동안 시간이 지남에 따라 4세 미만, 5-9세, 10-14세, 15세에서 69세 그리고 70세 이상의 사람들 중에서 로타바이러스에 감염되는 비율에 관한 회귀식을 수립합시다.

그림을 보면 시기별 바이러스의 변동은 주기성을 가지고 변화합니다. 이를 반영하여 비선형회귀모형을 generalized linear model로 구축할 필요가 있습니다.

만약 MGLM 패키지가 설치되어 있지 않으면
> install.packages("MGLM")

> require(MGLM)
# Fit multivariate response GLM regression
# dist = a description of the error distribution to fit
# MN = Multinomial Distribution
# DM = Dirichlet Multinomial distribution

> Multinom_mod <- MGLMreg(as.matrix(RotaVirusBB[, agNames]) ~
                          t + sin + cos, data = RotaVirusBB, dist = "MN")

as.matrix(RotaVirusBB[,agNames])에 agNames가 정의된 벡터로부터 필요한 열을 추출하여 행렬로 만듭니다. Y변수들의 행렬이 되겠네요. 각각에 대해 독립변수의 모형으로 시간(t), 주기변동(sin+cos)을 반영한 모형을 수립하고, distribution을 multinomial(MN)으로 해서 돌려봅시다.

열은 agNames가 행은 상수, t, sin, cos 이렇게 나옵니다. 모형의 wald value와 Pr로 봤을 때 일단 결과가 데이터를 잘 설명한다고 보입니다. 70세 그룹이 나오지 않는 것은 이것을 추정의 기반(base)으로 삼기 때문입니다.

t 값을 보면 negative이네요...

exp(-0.018) = 0.9823

exp(-0.011) = 0.9892

...

등이로 4세 미만, 5세 이상 9세 미만,...

이런 식으로 odd ratio를 구해봅시다. 결론적으로 70세보다(=1) 낮은 값이니 시간이 지남에 따라 70세 노년층 인구가 로타바이러스에 더 취약해지고 있다는 사실이 보입니다.

이를 Dirichlet-multinomial model로 구해봅시다.

> Dirichlet_mod <- MGLMreg(as.matrix(RotaVirusBB[, agNames]) ~
                          t + sin + cos, data = RotaVirusBB, dist = "DM")

그 결과를 보면

베이지안 추론이기에 70+ 이상도 보이고(base가 필요없습니다) 비교도 쉽지요.

모델 간 비교를 통해 어느 쪽이 더 나은 것인지 비교해 봅시다.

> Multinom_mod$AIC

> Multinom_mod$BIC

> Dirichlet_mod$AIC

> Dirichlet_mod$BIC

각각의 모형에 대해서 결과를 비교하면

AIC와 BIC가 더 작은 쪽이 간결하면서 설명력이 있습니다. 따라서 DMR이 선호됨.

ㅋㅋ